입력하다
- 힙은 최대값과 최소값이 항상 루트로 존재하는 트리입니다.
- 힙 트리에는 다음과 같은 속성이 있습니다.
- 힙 트리의 루트에는 최대값(max-heap의 경우) 또는 최소값(min-heap의 경우)이 있습니다.
- 힙 구조에서 상위 노드는 하위 노드보다 작거나(최소 힙의 경우) 커야 합니다(최대 힙의 경우).
- 힙 트리는 완전한 이진 트리입니다.
- 트리에 데이터를 입력하거나 삭제할 때 최대값과 최소값만 위로 이동하고 그렇지 않으면 정렬이 되지 않습니다. 이를 안티 얼라인먼트 조건이라고 합니다.
- 중복 값을 입력할 수 있습니다.
- 루트가 항상 최소가 되는 힙을 최소 힙이라고 하고 루트가 항상 최대가 되는 힙을 최대 힙이라고 합니다.
힙의 구현
- 이번에 구현할 힙은 최소 힙으로 구현되며 다음과 같은 동작을 갖는다.
- 데이터 붙여넣기
- 데이터 삭제
- 힙에서 항목 출력
- 힙은 전체 이진 트리의 속성을 가지므로 배열로 쉽게 구현할 수 있습니다.
- 기본 힙 구조는 다음과 같습니다.
import java.util.*;
// min Heap
class MyHeap{
ArrayList<Integer> heap;
MyHeap(){
heap = new ArrayList<>();
heap.add(-1);
}
public void add(int data){
}
public int remove(){
}
public void printTree(){
for (int i = 1; i < heap.size(); i++){
System.out.print(heap.get(i) + " ");
}
System.out.println();
}
}
힙에서 데이터 삽입
- 힙에 데이터를 삽입하는 방법은 다음과 같습니다.
- Full Binary Tree의 특성에 따라 데이터가 삽입된다. 즉, 데이터는 왼쪽에서 오른쪽으로 삽입됩니다.
- 그런 다음 삽입된 위치부터 부모 노드와 값을 비교하여 위치를 변경합니다. 위치 변경은 클러스터의 부모 노드가 자식 노드보다 작아야 한다는 조건을 만족합니다.
- 아래와 같이 트리에 6을 넣었습니다. 완전한 이진 트리의 특성에 맞게 삽입되었음을 알 수 있습니다.
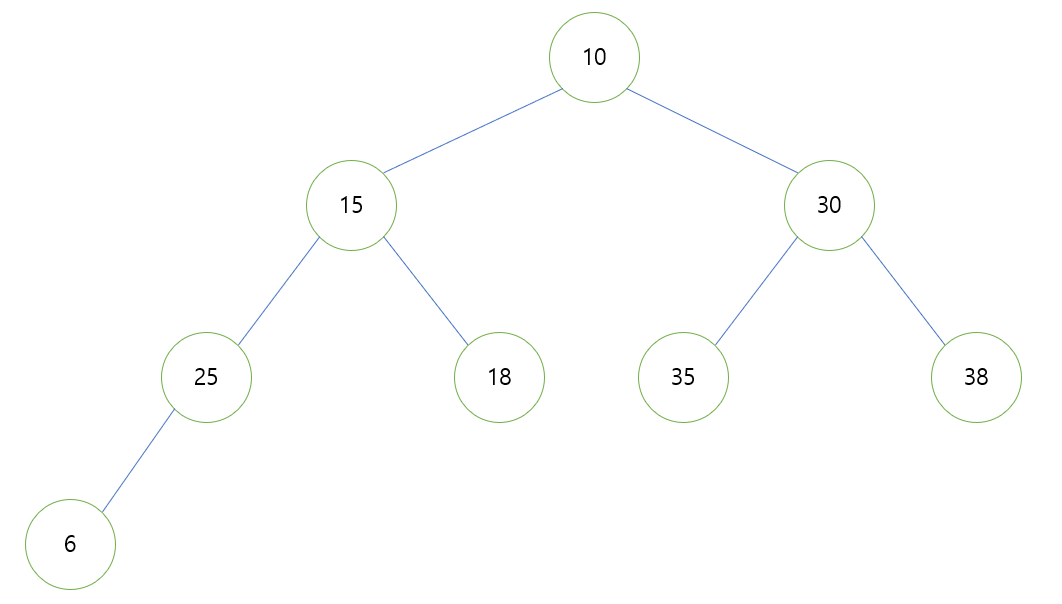
- 그런 다음 부모 노드가 자식 노드보다 작아야 한다는 원칙을 유지하기 위해 부모 노드와 값을 비교합니다.
- 여기서 그 값을 25와 비교하는데 25보다 작기 때문에 두 노드의 위치(값)가 바뀌게 된다.
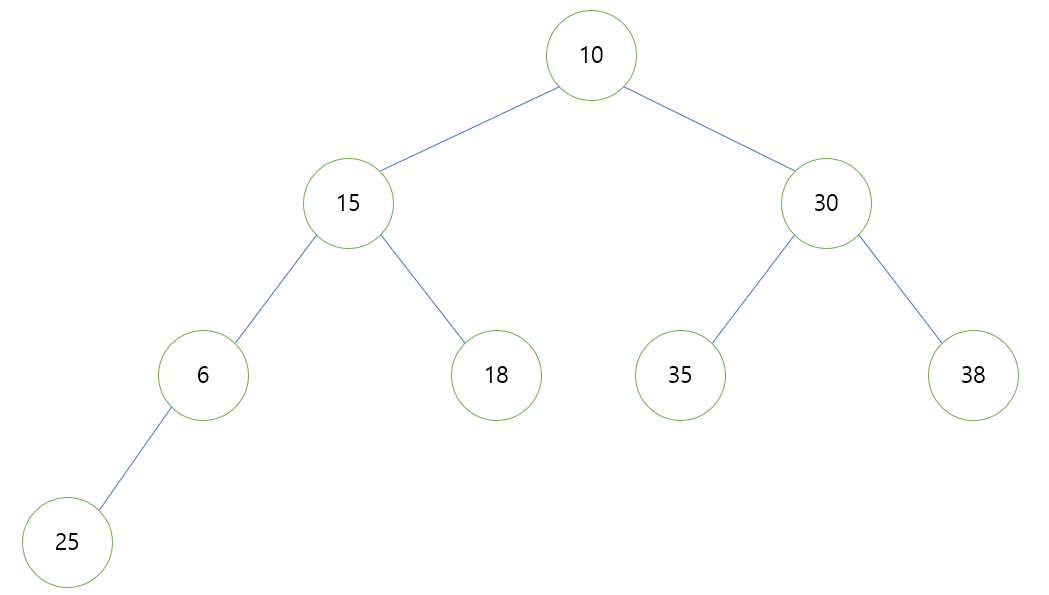
- 이제 다시 부모와 비교하여 부모보다 큰 위치가 생성될 때까지 위치를 이동합니다.
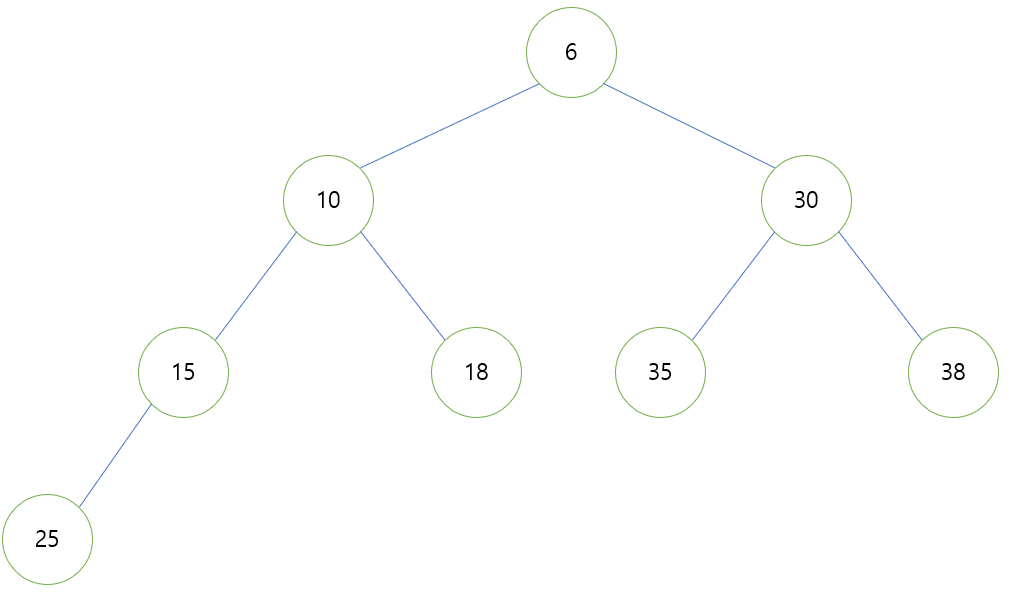
- 이것으로 최소 힙에 노드 삽입이 완료됩니다.
- 코드 구현은 다음과 같습니다.
public void add(int data){
heap.add(data);
int cur = heap.size() - 1;
// heap 에 들어간 데이터가 루트가 아니고 부모보다 내가 작은 동안 나는 위로 올라간다.
while(cur > 1 && heap.get(cur / 2) > heap.get(cur)){
int parentValue = heap.get(cur / 2);
// swap
heap.set(cur / 2, data);
heap.set(cur, parentValue);
// 이동했을 시 위치 갱신
cur /= 2;
}
}- 완전한 이진 트리에 인덱스가 있는 경우 index/2가 실행되는 위치는 해당 노드의 부모 노드라는 점을 기억하십시오.
- 관련 사항을 인식하는 한 나머지는 위의 구현에 불과합니다.
힙에서 데이터 지우기
- 다음과 같이 힙에서 데이터가 지워집니다.
- 루트에 있는 값을 반환하고 루트의 힙에 가장 최근에 삽입된 데이터를 배치합니다.
- 그런 다음 최소 힙에 맞게 비교하고 데이터 위치를 이동합니다.
- 이때 왼쪽 자식만 있는 경우와 자식이 둘인 경우 두 가지 경우가 있다.
- 왼쪽 자식만 존재하는 경우 데이터의 위치를 왼쪽 자식으로 보낸다.
- 자식이 두 개인 경우 두 자식 중 더 작은 값의 자식과 데이터를 비교하고 위치를 바꿉니다.
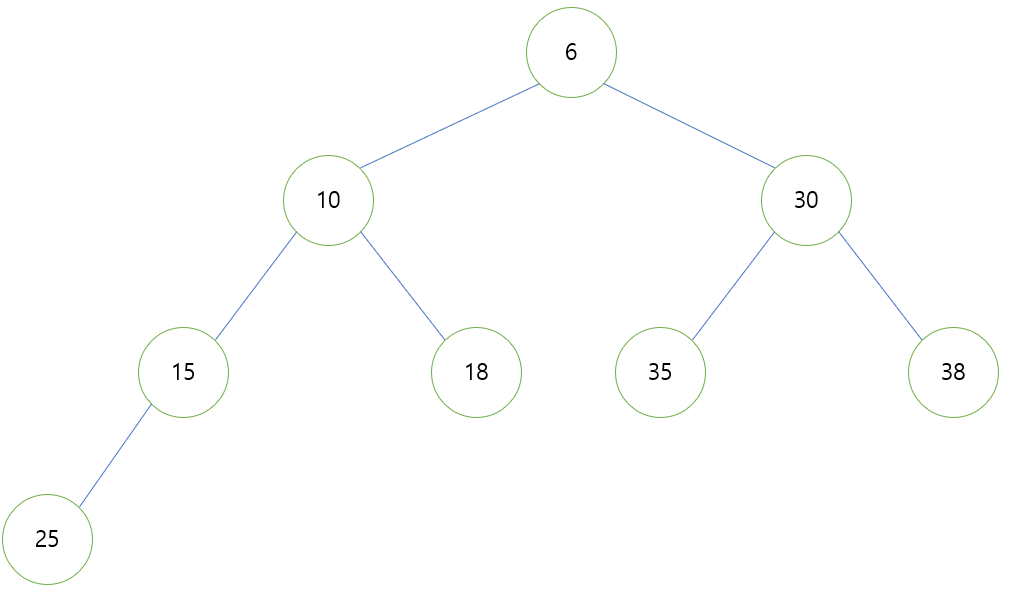
- 힙에서 데이터를 삭제합시다. 6을 반환하고 마지막 25를 루트로 올립니다.
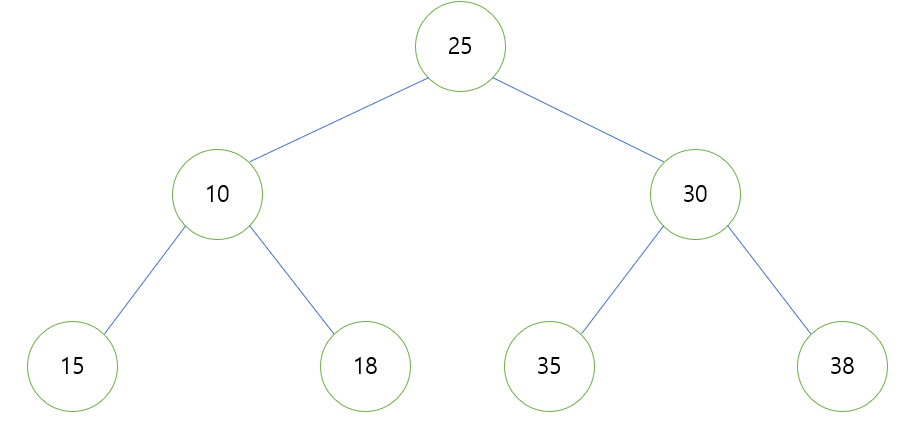
- 이제 그 값이 자식 노드보다 작도록 부모 노드의 위치를 변경합니다. 이 시점에서 25는 10과 30의 두 자녀를 가집니다. 이 경우 위에서 설명한 것처럼 10과 30 중 더 작은 것과 비교됩니다. 즉, 10과 비교됩니다.
- 10은 25보다 작기 때문에 25, 10은 위치를 교환합니다.
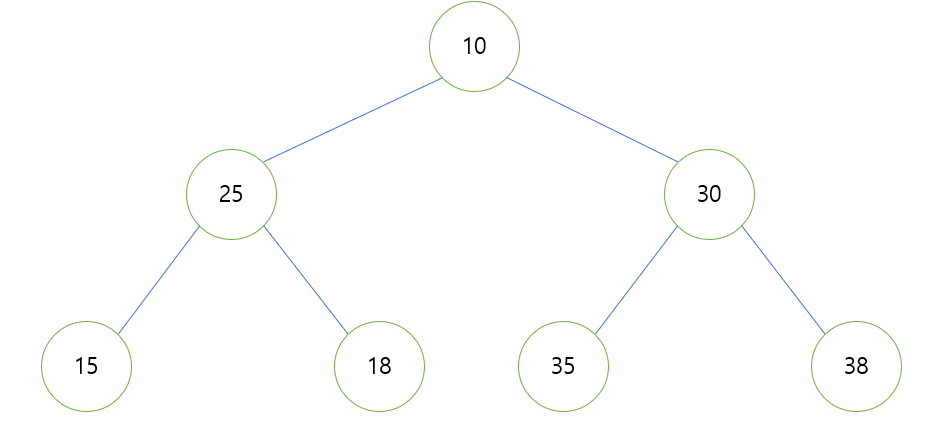
- 그런 다음 아이와의 비교는 낮은 위치에서 다시 발생합니다. 자식이 둘이니 15세나 18세 중 작은 것과 비교하고, 15세가 작으니 입장이 바뀐다.
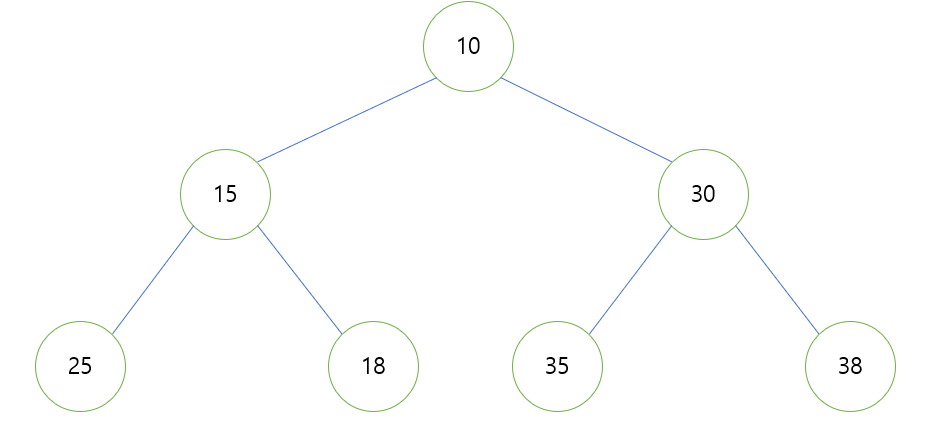
- 이것을 코드로 번역하면 다음과 같습니다.
public int remove(){
if (this.heap.size() == 1){
return -1;
}
int data = this.heap.get(1);
this.heap.set(1, heap.get(heap.size() - 1));
this.heap.remove(heap.size() - 1);
int cur = 1;
while(true){
int left = cur * 2;
int right = cur * 2 + 1;
int location = -1;
if (right < heap.size()){
location = heap.get(left) < heap.get(right) ? left : right;
} else if (left < heap.size()){
location = left;
} else{
break;
}
if (heap.get(cur) < heap.get(location)){
break;
} else{
int parentVal = heap.get(cur);
heap.set(cur, heap.get(location));
heap.set(location, parentVal);
cur = location;
}
}
return data;
}
정리하다
- 데이터를 삽입하고 삭제할 때 부모 노드의 크기가 자식 노드의 크기보다 작아야 한다는 원칙만 지키면서 최소 힙을 구현하는 것은 어렵지 않다.
- 최대 힙은 크기 비교의 역수만 필요하므로 구현하기가 그리 어렵지 않습니다.
- 전체 코드는 다음과 같습니다.
import java.util.*;
// min Heap
class MyHeap{
ArrayList<Integer> heap;
MyHeap(){
heap = new ArrayList<>();
heap.add(-1);
}
public void add(int data){
heap.add(data);
int cur = heap.size() - 1;
// heap 에 들어간 데이터가 루트가 아니고 부모보다 내가 작은 동안 나는 위로 올라간다.
while(cur > 1 && heap.get(cur / 2) > heap.get(cur)){
int parentValue = heap.get(cur / 2);
// swap
heap.set(cur / 2, data);
heap.set(cur, parentValue);
// 이동했을 시 위치 갱신
cur /= 2;
}
}
public int remove(){
if (this.heap.size() == 1){
return -1;
}
int data = this.heap.get(1);
this.heap.set(1, heap.get(heap.size() - 1));
this.heap.remove(heap.size() - 1);
int cur = 1;
while(true){
int left = cur * 2;
int right = cur * 2 + 1;
int location = -1;
if (right < heap.size()){
location = heap.get(left) < heap.get(right) ? left : right;
} else if (left < heap.size()){
location = left;
} else{
break;
}
if (heap.get(cur) < heap.get(location)){
break;
} else{
int parentVal = heap.get(cur);
heap.set(cur, heap.get(location));
heap.set(location, parentVal);
cur = location;
}
}
return data;
}
public void printTree(){
for (int i = 1; i < heap.size(); i++){
System.out.print(heap.get(i) + " ");
}
System.out.println();
}
}
public class StudyCode {
public static void main(String() args){
MyHeap heap = new MyHeap();
heap.add(10);
heap.add(25);
heap.add(24);
heap.add(13);
heap.add(7);
heap.printTree();
System.out.println(heap.remove());
System.out.println(heap.remove());
heap.printTree();
}
}